
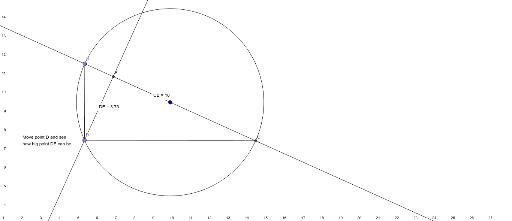
So let's solve it between equation seven an equation eight So X equals zero and y equals 1/3 times X plus for it simultaneously. Sure, so to do this, we're solving for this system of equations. In order to verify this point to make sure that it's actually at this location, I will get an exact value that we could be. That's what we're indicated to do in part C. Now our graphing calculator tells us that our or the center is at zero comma 1.33 Let's also find it Algebraic Lee. So we now have all of our altitudes and we can see we have this north of center here. So are why coordinate Here is zero, so we don't put it and our export it is too. And then we're also using points of this time with point B. So to be perpendicular are so please to be negative 2/3 the opposite or cyclical. So we hade a slope of three halves for a C. And then for this next altitude again we will go back to the slope from earlier. So this isn't point some form, though you could also of course, converted to any other form That's easy to breath. So this is actually like having a wine might zero here and then x minus here a good four turned into X plus four. Then, to complete the equation, we use point slip form So we have this point negative for common zero. So our slope here to be perpendicular must be 1/3. We know our slope here is negative three. Don't you have the questions for the other sides to do this one? We take a look at the equation from C to B, which we got earlier. X equals zero so that it makes a right and gold with white cool Syria. So we know here that this is going to be the equation.
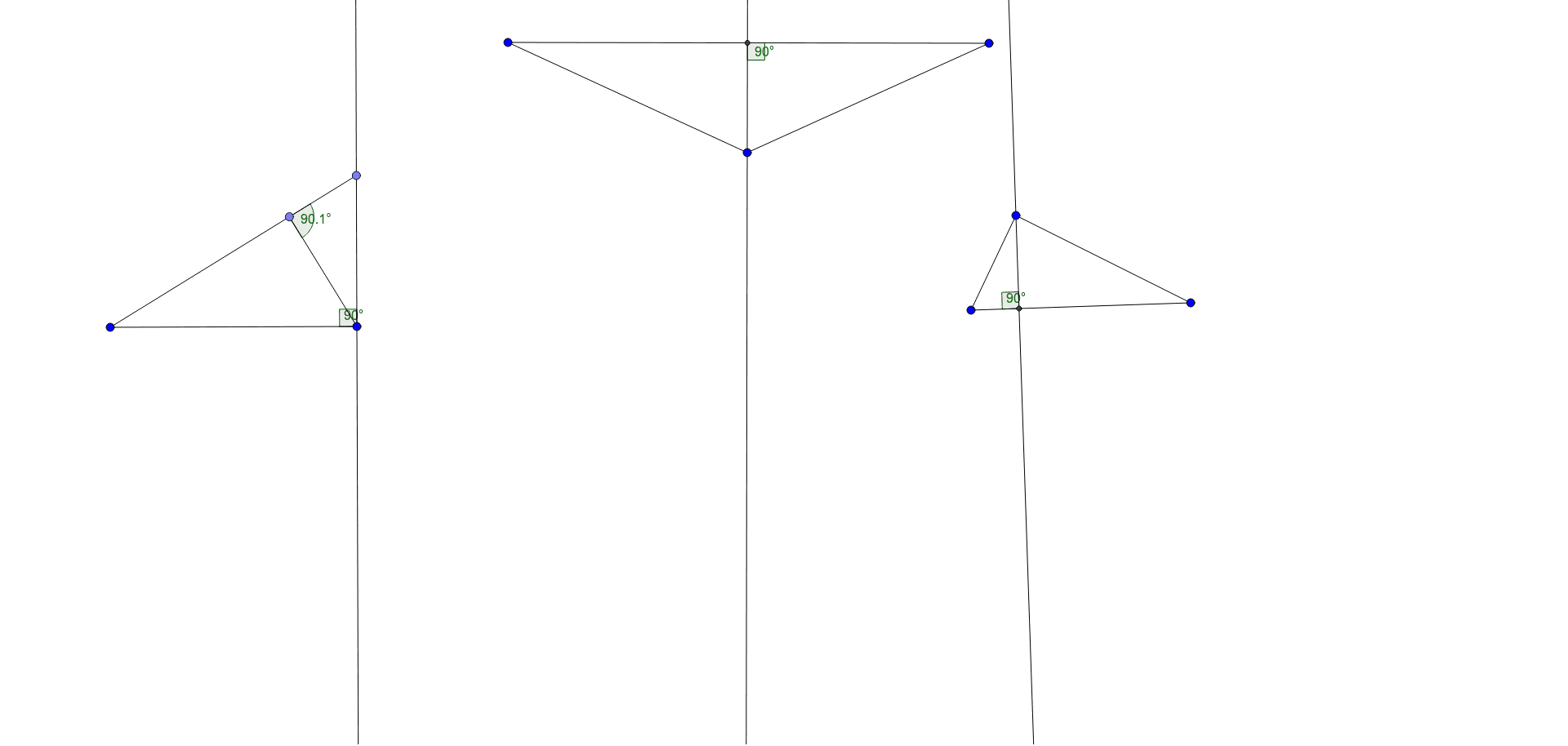
It goes from a vertex and makes a right and go out with the opposite soft. So here is our triangle and the equations for the lines that connect this triangle. We have a Y intercept of six and we have a slope of 6/4 or three house after simplifying. Here, going from a to B, we're just at y equals zero were right only because access and going from a to see. It just about the lines don't go too far out of their triangle into this process. So why equal six Ministry X is the equation for the mind segment here, and we have this text here.
So this abrasion going from sea to be we can tell that the white intercept here is six on that are slope is negative six over to or negative three. So we have to actually create equations for you to have the sides. So here on this craft we have these planes A, B and C that will form a triangle.
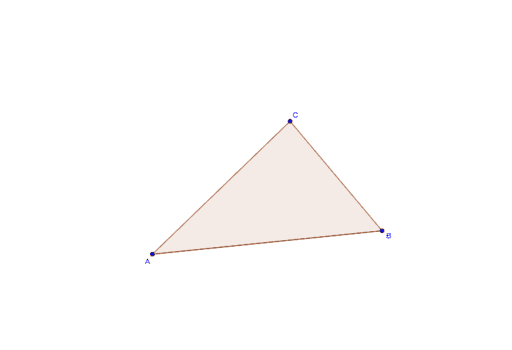
Are your estimates in part (b) close to these values? (c) Using simultaneous equations (from intermediate algebra), find the exact coordinates of the orthocenter. Use the graphing utility to estimate the coordinates of this point. Note that the altitudes appear to intersect in a single point. (b) Use a graphing utility to draw $\triangle A B C$ along with the three altitude lines that you determined in part (a). (Actually, you are finding equations for the lines that coincide with the altitude segments.) (a) Using paper and pencil, find the equations for the three altitudes. $ Note that one of the altitudes of this triangle is just the portion of the $y$ -axis extending from $y=0$ to $y=6 $ thus, you won't need to graph this altitude it will already be in the picture. This exercise illustrates the fact that the altitudes of a triangle are concurrent. The three altitudes of a triangle are concurrent the point where the altitudes intersect is the orthocenter of the triangle. A line segment drawn from a vertex perpendicular to the opposite side is an altitude. This point of intersection is called the centroid of the triangle. The three medians of a triangle are concurrent that is, they intersect in a single point. In a triangle, a line segment drawn from a vertex to the midpoint of the opposite side is called a median. You $\%$ need to recall the following definitions and results from elementary geometry. Please! I need your help! You will need to use Geogebra for this Related to the slope and angle of inclination of the original line? Measure its slope and angle of inclination. Values related to those values of the original line? ExplainĬonstruct a line perpendicular to your original line, and Slope and angle of inclination of this new line. How are the slope and the angle of inclination related? (Hint:Ĭonsider the triangle formed by your line and the two axes)’Ĭonstruct another line parallel to your line.
Altitude geometry geogebra update#
Vary the line and have the calculations update automatically. This is theĪngle of inclination for this line. Measure the angle between the x-axis and your line. Values to calculate the slope of the line. Points (the x-coordinates and the y-coordinates) and use these Measure the individual coordinates of the intersection Find the points of intersection of your line with SOLVED: Please! I need your help! You will need to use Geogebra for thisĭraw a line that intersects the negative x-axis and the


 0 kommentar(er)
0 kommentar(er)
